Сложный процент

            Сложным процентом принято называть эффект, возникающий при накоплении прибыли и процентов, в результате чего выплаты по процентам возрастают по экспоненциальному графику. Большинство современных банков принимают вклады клиентов именно под сложные проценты, что, несомненно, выгодно для вкладчика. Важность открытия сложных процентов оценил даже сам Эйнштейн, назвав их главной «движущей силой в мире».

            Для того чтобы лучше разобраться, что представляют собой сложные проценты, необходимо перейти к примерам с расчетами.

Как рассчитывается сложный процент?

            Для расчета применяется простая формула:

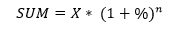
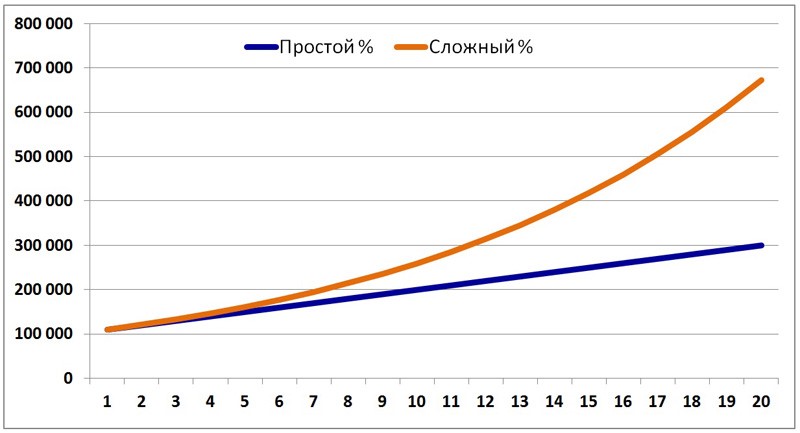
            В формуле под SUM понимается окончательная сумма расчета с клиентом, под Х –сумма вложения, под n – количество расчетных периодов. На графике можно увидеть, что подразумевается под экспоненциальным возрастанием суммы:

            Для банковских вкладов формула немного сложнее, так как вводится новый элемент уравнения – капитализация:

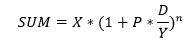
            Так, нам нужно знать частоту капитализации. Под капитализацией понимается перерасчет суммы, на которую начисляются проценты – к базовой сумме добавляется прибыль, начисленная за последний период. Если перерасчет происходит ежемесячно, частота капитализации (в нашей формуле это D) составляет 30 дней, если раз в квартал – 90 дней.

            Остальные незнакомые показатели в формуле расчета банковского сложного процента – это Y – количество дней в году (365 или 366) и P – процентная ставка. Весь блок значений после единицы под скобкой называется коэффициентом процентной ставки.

            Рассмотрим пример:

            Гражданин И вкладывает 100000 рублей под 15% годовых с ежемесячной капитализацией. Какую сумму он сможет получить через 8 лет:

А) с простого процента?

Б) со сложного процента?

            Так, рассчитываем сначала простой процент. 15% от 100000 рублей составляет 15000 рублей. Если 15 тыс. рублей умножить на 8, то получится прибыль с вклада в 120 тыс. рублей. Таким образом, через 8 лет гражданин И сможет снять 220 тыс. рублей.

            Для расчета сложного процента подставляем данные в формулу:

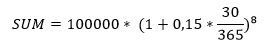
            Результат расчетов должен неприятно удивить – прибыль составит те же 120 тыс. рублей. Тогда попробуем рассчитать сумму при ежегодной капитализации, а не при ежемесячной:

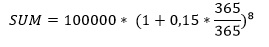
            Мы получим результат, который удовлетворит нас гораздо больше – 306 тыс. прибыли. Делаем вывод: чем реже происходит капитализация, тем выше будет прибыль. Проценты начисляются ежегодно таким образом:

            Видно, что под сложным процентом деньги растут словно снежный ком. Чем дольше вкладчик не будет их снимать, тем больше будет его прибыль от месяца к месяцу.

Другие полезные формулы

            Для расчетов по вкладам могут пригодиться и другие формулы:

1. Процентная ставка. Формула показывает, под какой процент нужно внести средства, чтобы получить желаемый результат.

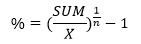
Все показатели нам известны, поэтому попробуем сразу решить пример:

Под какой процент нужно положить 10000 рублей, чтобы через 15 лет получить 80000 рублей?

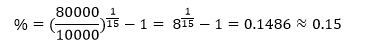
Понятно, что нужно положить деньги под 15% годовых.

2. Количество периодов. Формула показывает, на какое количество процентных периодов нужно внести средства, чтобы достичь желаемого результата:

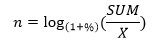
Опять-такие пробуем решить пример:

На сколько времени нужно внести деньги под 20% годовых в размере 150000 тыс. рублей, чтобы получить 1 млн. рублей?

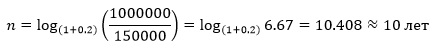
Нужно внести средства на 10 лет.

Правило 72

Существует правило, которое позволяет производить простейшие расчеты без степеней и логарифмов – правило 72. Оно гласит, что, разделив число 72 на процентную ставку по вкладу, мы можем определить время, за которое сумма на банковском счету удвоится. Так, например, при вложении под 36% годовых сумма увеличится в два раза уже через два года, а при вложении под 8% ждать удвоения придется целых 9 лет.

Эксперты рекомендуют производить вышеописанные расчеты еще перед посещением банка, однако, не каждый калькулятор может вычислить корень 15 степени или логарифмы. Выполнять расчеты можно на листе Excel либо, если вы не владеете этим инструментом, воспользоваться одним из готовых калькуляторов, например, на портале CalcSoft.ru.