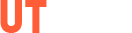В руках математиков компьютеры могут оказаться ценным инструментом. Однако машины могут также играть свою собственную роль в доказательстве математических теорем.
Первый крупный результат такого рода был получен 40 лет назад - в 1976 году. Тогда компьютер доказал теорему четырех красок, согласно которой любая карта (при некоторых условиях) может быть окрашена с использованием только четырех различных цветовых оттенков.
В 2003 году Томас Хейлз (Университет Питтсбурга) опубликовал компьютерное доказательства гипотезы Кеплера о том, что для расположения сферических объектов равного диаметра с точки зрения занимаемой ими площади всем известный метод укладки апельсинов в супермаркете является наиболее эффективным. Многих математиков доказательство, сделанное с помощью машины, не удовлетворило. Проверить его правильность было практически невозможно, так как вычисления занимали два гигабайта, а для 2003 года это была огромная цифра.

Теорема четырех красок в наглядном представлении
Свежие примеры исследований
Недавно журнал Nature опубликовал компьютерное решение булевой проблемы пифагоровых "троек". Суть ее заключается в том, что целые числа от одного до 7 824 могут быть окрашены в красный или синий цвет. При этом среди целых чисел (a, b и c) не будет ни одной "тройки" из чисел одинакового цвета, которые можно было бы подставить в знаменитую формулу теоремы Пифагора, где a, b и c - стороны прямоугольного треугольника. Булевая проблема пифагоровых "троек" верна только для диапазона чисел от 1 до 7 825.
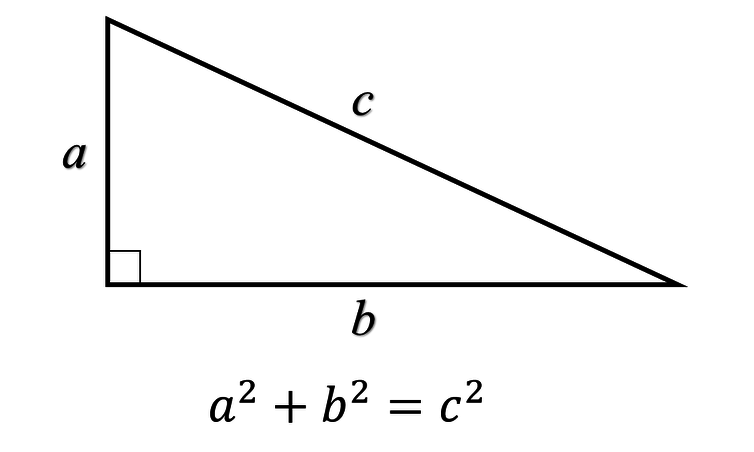
Теорема Пифагора для прямоугольного треугольника
Как оказалось, число возможных цветовых вариантов для целых чисел от 1 до 7 825 составляет более 10 в 2,300-й степени . Оно намного превышает количество элементарных частиц в видимой вселенной, которое равно всего лишь 10 в 85-й степени.
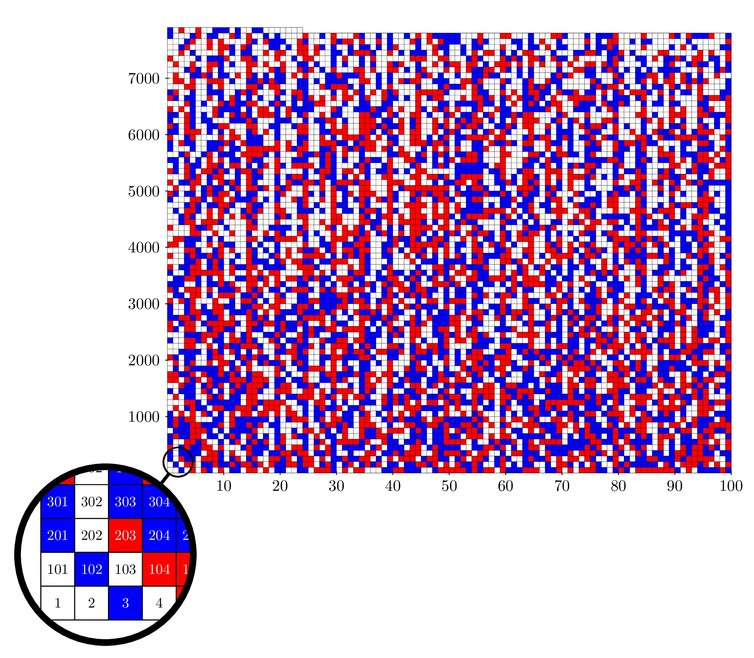
Числа от 1 до 7 824 можно покрасить в красный или синий цвет, и ни одна тройка a, b и c из чисел одинакового цвета не будет удовлетворять теореме Пифагора. Белый квадрат может быть красного или синего цвета
Ученые смогли сократить варианты до одного триллиона, воспользовавшись свойствами теории чисел и различными симметриями. Суперкомпьютер Stampede, находящийся в Университете штата Техас, изучил каждый из триллиона случаев, на что ему потребовалось два дня. По самым приблизительным подсчетам для решения теоремы булевых пифагоровых троек понадобилось 10 в 19-й степени арифметических операций.
Но это далеко не предел. Например, в рамках масштабного проекта по поиску простых чисел Мерсенна (GIMPS) выполняется, в общей сложности, около 450 триллионов вычислительных операций в секунду.
Пора ли списывать математиков в утиль?
Совсем нет. Математики, как и многие другие специалисты, пользуются в своей работе новыми методами исследования. В частности, они разрабатывают так называемую экспериментальную математику, за которой стоит большое будущее. Что такое экспериментальная математика? Это способ исследования, при котором компьютеры используются в качестве "лаборатории".
Экспериментальная математика, базирующаяся на компьютерных вычислениях сильна тем, что опирается на современную технологию. Но человеческий разум по-прежнему необходим для того чтобы проверять результаты математических вычислений и доказательств. Компьютер же помогает математикам выявлять новые теоремы и определять пути к их формальному доказательству. Более того, во многих случаях компьютерные вычисления являются более убедительными, чем те, которые выполнил человек. Человек может ошибиться, что-то упустить, понадеяться на предыдущие результаты, которые могут оказаться несостоятельными.
Например, в первоначальном доказательстве Великой теоремы Ферма, которое предоставил Эндрю Уайлс (Andrew Wiles), позднее были обнаружены ошибки. Впоследствии они были исправлены.
И еще один пример, недавно Александр Йи (Alexander Yee) и Шигэру Кондо (Shigeru Kondo) нашли 12,1 триллионов цифр числа "Пи". Для этого они пользовались разными компьютерными алгоритмами вычислений и в конце своей работы сравнили результаты. Результаты полностью совпали.
Так какой результат является более надежным? Тот, который сделан человеком, расписавшим доказательство теоремы на многие сотни страниц, проверить которые смогут всего несколько других математиков, или результат компьютерных арифметических вычислений, как в случае Йи-Кондо? Вывод очевиден: результат, полученный с помощью компьютера, будет во многих случаях более надежным.
Что будущее нам готовит?
Есть все основания утверждать, что в будущем математики в своих исследованиях будут широко использовать вычислительную мощь компьютеров.
Вопрос о роли компьютеров уже не раз поднимался математиками. В очередной раз он был обсужден в июне 2014 года на конференции, где выступили пять претендентов на получение премии Breakthrough Prize in Mathematics (Премия за прорыв в математике). Австралийско-американский математик Теренс Тао (Terence Tao) сказал буквально следующее:
"Безусловно, компьютеры становятся все мощнее, но я ожидаю, что большая часть математики будет по-прежнему делаться людьми, работающими на компьютерах".
Так что пока не выбрасывайте свой учебник алгебры. Он вам еще пригодится!
Открыть счет для торговли акциями высокотехнологичных компаний