Модели ценообразования опционов – это модели, объясняющие случайный порядок формирования стоимости опциона. Трейдеры и инвесторы активно используют такие модели для расчета потенциальной прибыли от сделки с опционом.
Эффективных моделей ценообразования опционов не существовало вплоть до 1973 года, когда появилась CAPM – модель ценообразования долгосрочных активов. Проблема этой модели заключалась в ее узком применении – она позволяла оценивать только рискованные активы. На настоящий момент существует большое количество более универсальных моделей, среди которых выделяются следующие:
Модель Блэка-Шоулза
Модель Блэка-Шоулза считается наиболее распространенной моделью ценообразования опционов – гипотеза авторов заключается в том, что если базисный актив торгуется на рынке, то и цена самого опциона на базисный актив диктуется рынком. Такая модель применима для оценки не только опционов, но и производных бумаг (например, варрантов) и собственного капитала фирмы.
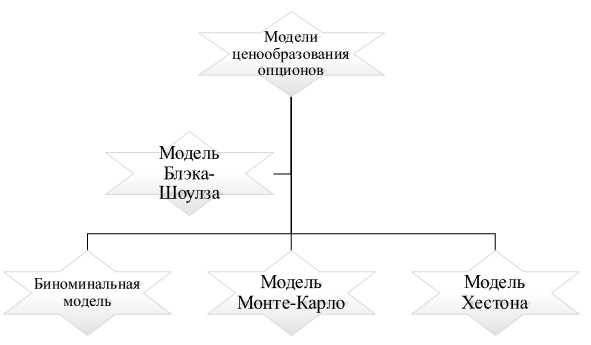
Блэк и Шоулз считали, что основным фактором ценообразования выступает будущая волатильность базиса опциона. Цена на опцион возрастает и падает прямо пропорционально стоимости базисного актива. Для вычисления цены опциона была создана формула, что явилось революционным шагом для 70-х годов – прежде математический подход к оценке деривативов не использовался:
С помощью такой формулы рассчитывается стоимость опциона Call. Стоит пояснить, что означают переменные в этом уравнении: S – цена базового актива, N – вероятность того, что отклонение в условиях стандартного распределения будет меньше (для расчета N можно использовать Excel – функция НОРМСТРАСП), K – цена, по которой опцион будет реализован на дату экспирации, r – безрисковая ставка, T-t – время, оставшееся до даты экспирации.
Для расчета стоимости опциона Put используется та же формула, только вычитаемое и уменьшаемое меняются местами.
Биноминальная модель
Биноминальная модель имеет в основе предположение, что цена опциона может принимать одно из двух значений: U – минимум и D - максимум. Основной формулой для расчета стоимости опциона выступает следующая:
Для расчета переменных используется ряд вспомогательных формул:
Уточним, что S0 – это стоимость базисного актива на дату приобретения опциона, следовательно, показатели d и u – это цены максимум и минимум опциона, приведенные к первоначальной стоимости базиса. Переменная E – цена, по которой опцион будет реализован в дату экспирации, t – весь период существования опциона (от покупки до экспирации) – измеряется t в годах.
Биноминальная модель позволяет произвести оценку опциона в любой момент времени до срока реализации опциона, чем и отличается от модели Блэка-Шоулза. Поэтому биноминальная модель используется для оценки американских опционов (которые инвестор может закрыть в любой момент), а модель Блэка-Шоулза – для европейских опционов.
Модель Монте-Карло
Модель Монте-Карло предполагает оценку математического ожидания выплаты по всей истории базиса. Такая модель считается одной из самых сложных и используется тогда, когда остальные модели неприменимы.
Суть модели можно объяснить на примере игрального кубика. Математическое ожидание числа очков на кубике, вычисленное способом суммирования значений, составит 3.5. Если мы бросим кубик, допустим, 1000 раз и посчитаем среднее, то получим близкое значение, например, 3.505 или 3.497. При том чем больше бросков (применяется термин «итерации»), тем выше точность. Так же и с опционами – инвестору следует сгенерировать как можно большее число итераций цен базиса и посчитать среднее. Расчет будущей цены происходит по формуле:
В этой формуле t – момент времени (например, t = 1 обозначает цену опциона через год), S0 – настоящая цена базиса,
u – ожидаемая доходность базиса, выражаемая в процентах, o – отклонение доходности (также называется волатильностью), выражаемое в процентах. N0,1 – случайная величина. Сгенерировать случайную величину можно при помощи Excel.
Модель Хестона
Модель Хестона исходит из гипотез, что распределение цен активов может отличаться от логарифмически нормального и что волатильность может быть случайной. Модель Хестона применима только для опционов европейского типа. Она представляет собой систему уравнений:
Первое уравнение является основным, а второе задает дисперсию. Параметры имеют такой смысл:
- X – цена опциона (X0 – первоначальная цена).
![]() – равновесное вероятное отклонение.
– равновесное вероятное отклонение.
![]() – скорость возвращения к равновесному отклонению.
– скорость возвращения к равновесному отклонению.
Модель Хестона, как и модель Монте-Карло, принадлежит к числу сложных моделей – для их расчета следует применять специализированные программы, так как ручной расчет потребует много времени и знаний. Именно из-за сложности альтернатив модель Блэка-Шоулза пользуется такой популярностью.
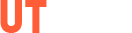
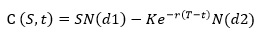
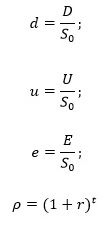
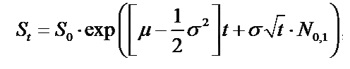
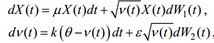
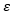
В бинарной модели перепутали описание переменных, нужно: U – максимум, D - минимум