В прошлой части мы рассмотрели оптимальное управление inventory risk в маркетмейкерском алгоритме. Напомню, что формулы для нейтральной цены и оптимального спреда между лимитными ордерами были получены при допущении, что цена следует геометрическому броуновскому движению. Управление inventory risk для моделей цены, более приближенными к реальности, рассматривается, например, в статье Pietro Fodra & Mauricio Labadie «High-frequency market-making with inventory constraints and directional bets» . Однако, применить напрямую на практике алгоритмы из этих статей вряд ли получится, так как в них не учитывается действие adverse selection risk. Поэтому в данной части рассмотрим работу JIANGMIN XU «Optimal Strategies of High Frequency Traders», в которой автор делает попытку учесть этот вид риска, конечно, наряду с inventory risk.
Для этого необходимо получить предсказание направления движения цены в коротком промежутке времени ( мы говорим о высокочастотных алгоритмах, поэтому такой промежуток будет измеряться в секундах, или даже долях секунды). JIANGMIN XU предлагает учитывать зависимость цены от дисбаланса объемов в стакане, который равен разности между логарифмами объема лучшей покупки и объема лучшей продажи F=log(Qbestbid)−log(Qbestask). Этот дисбаланс следует процессу Орнштейна-Уленбека с нулевым средним:
где αF- константа, отражающая скорость колебаний вокруг среднего,
σF- постоянная, отражающая волатильность процесса,
dWt- случайный броуновский процесс.
Далее нам понадобится модель спреда St- разницы цен между лучшим аском и лучшим бидом- которая представляет собой марковский процесс с тремя состояниями -S={δ,2δ,3δ}, где δ- шаг цены. Матрицу вероятностей переходов обозначим ρ=(ρi,j) 1≤i,j≤3, ρi,i=0.
В качестве модели прироста цены актива возьмем один из видов марковского процесса — pure-jump process :
dJ1t- первая составляющая имеет интенсивность скачков цены λJ1, величину скачка δ/2 с вероятностью ψ1(Ft) и величину скачка −δ/2 с вероятностью 1−ψ1(Ft),
dJ2t — вторая составляющая имеет интенсивность скачков λJ2, величину скачка δ с вероятностью ψ2(Ft) и величину скачка −δ с вероятностью 1−ψ2(Ft) ,
где функция ψi имеет форму
для i =1,2.
Дисбаланс объемов Ft в стакане влияет на скачок цены в следующий момент времени таким образом: если Ft>0 цена с большей вероятностью будет расти и наоборот. Этот сигнал конечно не идеален, но позволяет предсказывать цену на коротком временном промежутке и будет полезен для формирования формулы оптимального управления рисками в рамках HFT стратегии.
Сформулируем основные стратегии для HFT алгоритма:
1. Котирование (make strategy). В рамках этой стратегии алгоритм может располагать лимитные ордера на best bid или best ask, а если спред St>δ, то ордера могут располагаться на ценовых уровнях Pt−St/2+δ(Pt+St/2−δ), для увеличения вероятности взятия ордера с меньшими затратами, чем затраты при гарантированном исполнении маркет ордера. Эту модель представим в виде непрерывного процесса:
b и a означают bid и ask соответственно. Таким образом 0 означает постановку ордера на лучшую цену покупки или продажи, а 1 означает постановку ордера на лучшую цену плюс/минус δ. Если спред минимальный — St=δ — то значение 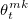 может быть равно только 0.
может быть равно только 0.
2. Использование маркет ордеров (take strategy). Для получения мгновенного исполнения алгоритм может использовать маркет ордера. Маркет ордер, в отличие от лимитного, забирает ликвидность из стакана и имеет высокую стоимость, равную половине спреда (без учета комиссии). Смоделируем данную стратегию как импульсный процесс в непрерывном времени:
где τn- возрастающая последовательность моментов времени, когда используется маркет ордер,
ζn ∈ {−ζmax,ζmax}- случайная переменная, представляющая число контрактов, купленных или проданных в эти моменты времени.
Для чего нужны все вышеописанные модели? Наша цель — составить уравнение оптимального контроля, в котором будет учтен как inventory risk, так и adverse selection risk. А решением этого уравнения будет матрица состояний, которую можно представить в виде графика с двумя осями значений — первая ось inventory level, это текущая открытая позиция, вторая ось — depth imbalance, то есть диcбаланс объемов в стакане. Таким образом эти оси значений представляют собой аргументы по которым происходит управление — по первой оси — inventory risk, по второй оси — adverse selection risk. Матрица состояний представляет собой множество значений 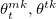 . Их можно представить на графике в виде области внутри квадрата, ограниченного рассмотренными осями значений. Такой график представлен в заглавии поста, для значения спреда St=δ, на момент времени t=10 (за единицу времени может быть принят любой интервал, в зависимости от требуемой частоты сделок). На графике выделены следующие области:
. Их можно представить на графике в виде области внутри квадрата, ограниченного рассмотренными осями значений. Такой график представлен в заглавии поста, для значения спреда St=δ, на момент времени t=10 (за единицу времени может быть принят любой интервал, в зависимости от требуемой частоты сделок). На графике выделены следующие области:
1. Market making — в этой области выставляются ордера как на покупку так и на продажу по ценам best bid и best ask, то есть 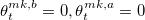 ;
;
2. Momentum (buy/sell). В этих областях необходимо срочное закрытие позиций, если они открыты в сторону, противоположную диcбалансу объемов и установление позиции согласно этому диcбалансу. Здесь используются маркет ордера, и θtk равен какому-то количеству контрактов, больше открытой позиции по модулю, противоположному по знаку.Точная величина зависит от значений на осях аргументов.
3. Inventory control (buy/sell). Эти области означают ликвидацию открытых позиций в ноль, также с использованием маркет ордеров, θtk равен открытой позиции с противоположным знаком.
4. Partial inventory control (buy/sell). Эти области аналогичны inventory control, но открытая позиция закрывается не полностью, θtk меньше открытой позиции по модулю, противоположна по знаку. Точная величина зависит от значений на осях аргументов.
В следующих статьях мы составим уравнение оптимального контроля и найдем его решение численными методами.
Источник - www.quantalgos.ru
 uralpro
uralpro 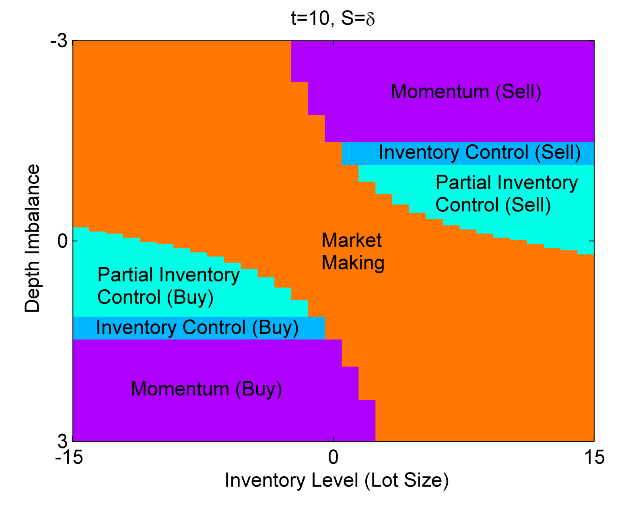
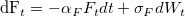
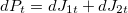
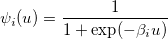
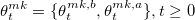
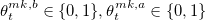
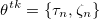


Все бы хорошо, но картинок с формулами не видно совсем.