Прошлые части цикла здесь. В этой части статьи мы найдем численное решение системы уравнений оптимального управления позицией маркетмейкера. Такое решение легко запрограммировать и использовать в реальной торговле для контроля за лимитными и маркет ордерами в соответствии с полученными стратегиями θmk,θtk. Для упрощения разложим функцию владения на слагаемые, чтобы получить сокращенную функцию владения v(t,y,f,s), которая представляет собой только динамическую составляющую основной функции:
Для v система уравнений выглядит следующим образом:
с терминальным условием:
Переходим к численному решению. Зададим на интервале [0,T] дискретную сетку времени t с равными интервалами 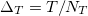 :
:
Также дискретизируем открытую позицию 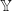 и дисбаланс объема
и дисбаланс объема 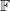 , с максимальными значениями
, с максимальными значениями 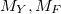 и шагами дискретизации
и шагами дискретизации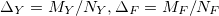 , где
, где
Далее, для вычисления численных производных по дисбалансу объема F, определим две дифференциальные матрицы — D1 для вычисления производной первого порядка и D2 — для вычисления производной второго порядка, на сетке 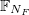 :
:
Обозначим оператор выбора для любой действительной функции 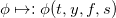 :
:
Оператор выбора имеет простой смысл: если некая функция ϕ максимальна при воздействии оператора 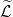 (что для функции владения соответствует использованию лимитных ордеров) или оператора
(что для функции владения соответствует использованию лимитных ордеров) или оператора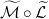 (использование маркет ордеров), то при текущих параметрах t,y,f,s выбирается именно эта политика (то есть лимитные или маркет-ордера).
(использование маркет ордеров), то при текущих параметрах t,y,f,s выбирается именно эта политика (то есть лимитные или маркет-ордера).
Выражения для операторов в фигурных скобках:
здесь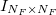 — матрица идентичности размерностью
— матрица идентичности размерностью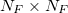 (матрица, где по главной диагонали расположены единицы, остальные элементы 0),
(матрица, где по главной диагонали расположены единицы, остальные элементы 0),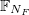 — столбец значений дисбаланса,
— столбец значений дисбаланса,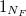 — единичный вектор размерностью
— единичный вектор размерностью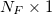 ,… означает поэлементное произведение векторов и матриц. Таким образом,
,… означает поэлементное произведение векторов и матриц. Таким образом,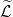 представляет собой вектор размерностью
представляет собой вектор размерностью 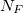 на сетке
на сетке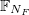 .
.
Аппроксимируем сокращенную функцию владения v численным решением w:
Полное решение для функции владения можно получить методом обратной индукции, который состоит из следующих последовательных шагов:
1. На конечный момент времени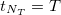 : для каждой комбинации значений (y,f,s) вычисляем
: для каждой комбинации значений (y,f,s) вычисляем 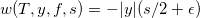 .
.
2. Начиная с момента времени tk+1 до момента tk, где k пробегает значения от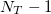 до 0 для каждой комбинации (y,f,s) делаем следующее:
до 0 для каждой комбинации (y,f,s) делаем следующее:
- Вычисляем
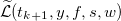 по вышеприведенной формуле и находим политику лимитных ордеров
по вышеприведенной формуле и находим политику лимитных ордеров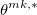
- Вычисляем
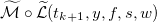 , и находим политику маркет ордеров
, и находим политику маркет ордеров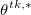
- Если
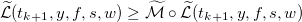 , то текущей политикой на момент времени tk выбирается
, то текущей политикой на момент времени tk выбирается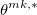 , при значениях (y,f,s), то есть в этот момент времени используюся лимитные ордера, согласно значению
, при значениях (y,f,s), то есть в этот момент времени используюся лимитные ордера, согласно значению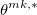 , которое, как мы помним означает выставление ордера, с количеством контрактов =1, или на лучший бид/аск, или перед/до него.
, которое, как мы помним означает выставление ордера, с количеством контрактов =1, или на лучший бид/аск, или перед/до него. - В обратном случае выбирается политика
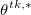 в момент времени tk при значениях (y,f,s), то есть используются маркет ордера с количеством контрактов, вычисленных в
в момент времени tk при значениях (y,f,s), то есть используются маркет ордера с количеством контрактов, вычисленных в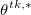
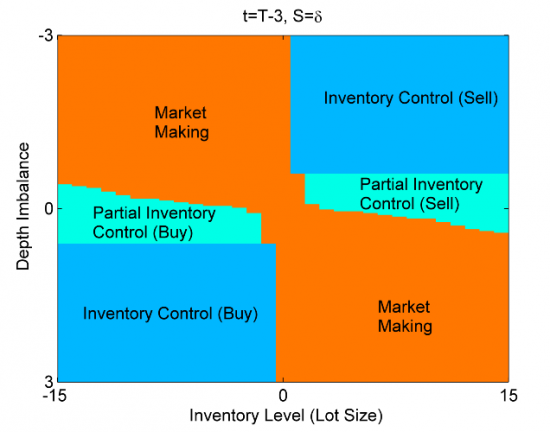
Таким образом, для всех значений времени t, всех значений открытой позиции y, всех значений дисбаланса объемов f и всех значений спреда s — (t,y,f,s)- мы определяем, какие ордера нам ипользовать в каждом случае, и формируем области, подобные указанным на графике в заглавии, где изображены политики при значениях спреда, равному шагу цены, и значению времени, меньше на 3 единицы (например, секунды) времени окончания торговли, для всех значений открытой позиции и спреда. Что означают эти области, вы можете посмотреть в части 2 и части 3 данного цикла статей. В следующей статье обсудим, как находить параметры в уравнении для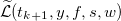 , основываясь на реальных биржевых данных, и начнем составлять код на C# для численного решения методом обратной индукции.
, основываясь на реальных биржевых данных, и начнем составлять код на C# для численного решения методом обратной индукции.
Источник - quantalgos.ru
 uralpro
uralpro 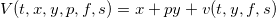
![Алгоритмы маркетмейкера. Часть 4 \max\left[\frac{\partial v}{\partial t}+y\frac{\mathbb{E}_t dP_t}{dt}+\mathcal{L}^F\circ v-\gamma y^2\frac{\mathbb{E}_t d[P,P]_t}{dt}+](http://mathurl.com/qe2xdad.png)
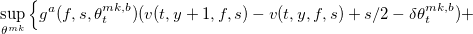
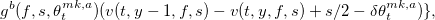
![Алгоритмы маркетмейкера. Часть 4 \sup\{v(t,y+\zeta,f,s)-|\zeta|(s/2+\epsilon)\}-v]=0](http://mathurl.com/n5uabuy.png)
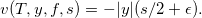
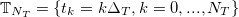
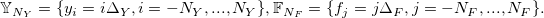
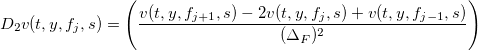
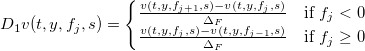
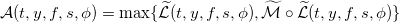
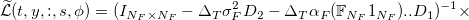
![Алгоритмы маркетмейкера. Часть 4 \Bigg(\phi(t,y,:,s)+\Delta_T y \frac{\mathbb{E}_t dP_t}{dt}+\Delta_T\mathcal{L}^S(\phi(t,y,:,s))-\Delta_T\gamma y^2\frac{\mathbb{E}_t d[P,P]_t}{dt}+](http://mathurl.com/kjrunym.png)
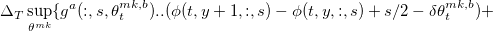
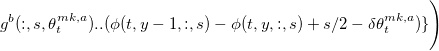
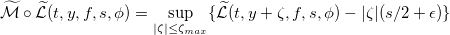
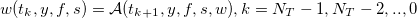


 Сделал примерно так же
Сделал примерно так же
И взорвалась голова