Misnik В этой статье, я изложу основу-основ статистического арбитража – коинтеграционный подход. Несмотря на то, что здесь уже была статья про коинтеграцию и парный трейдинг, я постараюсь изложить материал, чуть более системно, и может быть от этого более сложно. Но, зато надеюсь у Вас сложится комплексное понимание базового метода стат. арбитража. Возможно это будет циклом статей по базовым алгоритмам. Который приобщит еще большее количество людей к этому замечательному стилю торговли.
Что такое коинтеграция?
(и почему нам не так сильно важна корреляция)
Итак у нас есть две акции А и В и их цены за определенный период времени (временной ряд цен). Цены этих двух акций будут называться коинтегрированными, если они могут быть линейно скомбинированы в один ряд обладающий свойством стационарности.
Запишем это формулой. И затем разберем всё по порядку:
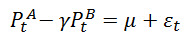
Итак, обозначим:
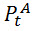– ряд цен акции А. Где t это время. Например если 16го марта акция «А» стоит 100 долларов. Это будет записано как:
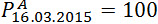
а если 14го марта она стоила 101 доллар, то мы это запишем как:
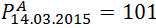
Но поскольку мы работаем с большим набором цен за определенный период, а не за какой то конкретный день, то цены акций А и B записываются как: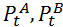 
Далее мы говорим
«если они могут быть линейно скомбинированы».
Что значит линейно?
Для простоты это когда мы складываем «+» или вычитаем «-» цену акции А из В или В из А. При этом можем цены одной из акций умножить на некоторое значение. Как видите в формуле цена акций B домножены на некоторый коэффициент γ (будет не совсем верно, но для простоты я пока буду называть коэффициент фиксированным числом, хотя на самом деле это ненулевой вектор). Так вот мы проводим нехитрую манипуляцию с ценами, домножаем цены акции B на какое то число и отнимаем эти цены от цен акций А.
Разжуем еще подробнее:
14го марта акция А стоила 101 рубль. Акция В 14го марта стоила 30 рублей.
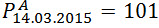
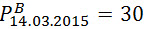
γ – мы вычислили что это число для этих акций, равно 2. (как вычислять мы поговорим ниже). На самом деле этот коэффициент называется коэффициентом коинтеграции.
Тогда мы имеем 14го марта:
101 – 2 * 30 = 41
Это называется линейной комбинацией. Думаю разобрались.
Пойдем далее:
«скомбинированы в один ряд»
Я привел пример для 14го марта. Но предположим что мы делаем такое вычитание цен(комбинируем) для каждого дня марта (с 1 марта по 16ое марта). Тогда каждый раз отнимая цены мы получим 16 чисел. Эти 16 чисел называются "временным рядом" только уже не самих цен, а их разности. И обозначаются как:
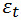
Идем далее:
«обладающий свойством стационарности»
Для простоты: стационарность это когда график постоянно ходит вокруг одного и того же значения:
Стационарный ряд:
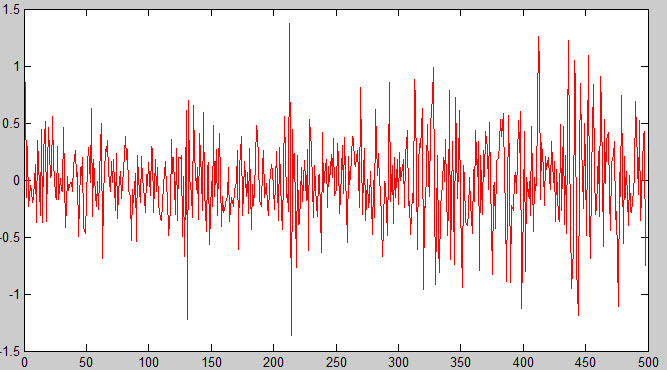
Нестационарный ряд:
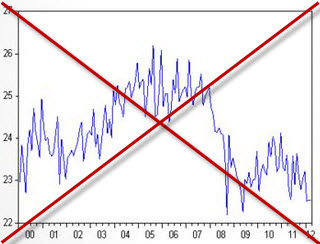
Стационарный:
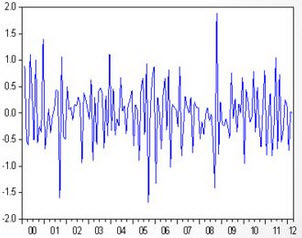
Нестационарный:
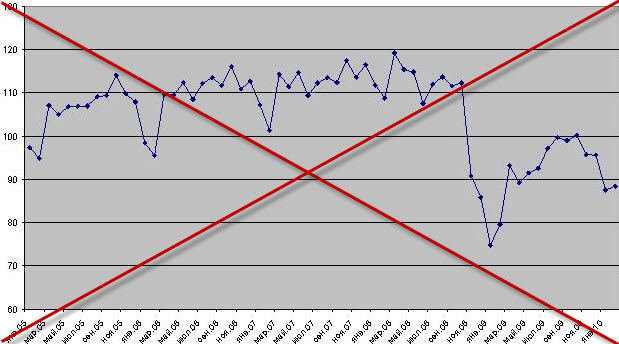
Если говорить правильно стационарность это когда вероятностные свойства постоянны.
Почему нам важно чтобы он был стационарным?
Да потому что его движение как видите из стационарных графиков выше легко предсказать.
ВАЖНО!
Стационарность это статистическое свойство! И например вот такой ряд мы не назовем стационарным:
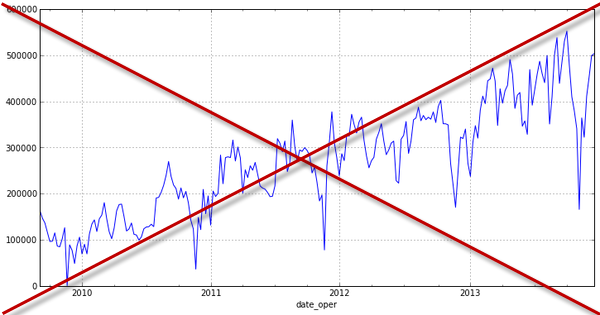
Несмотря на то, что вроде бы мы можем предсказать его движение (!).
ВАЖНО!
ДАЛЕКО не все пары инструментов (акций, фьючей и тд), могут быть коинтегрированы. Этим свойством обладают ограниченное количество инструментов на рынке.
ВАЖНО!
Для вычисления коинтеграции важно какой период времени мы возьмем. И какой таймфрейм. То есть например:
Пара: ISBC & STI коинтегрирована на промежутке 01-02-2012 – 01-03-2015 (по дневным закрытиям). Но не коинтегрирована на промежутке 01-01-2010 – 01-03-2015.
ВАЖНО!
Неспроста мы использовали в формуле тот самый коэффициент . Дело в том что сама по себе разность цен ISBC – STI как и обычные разности других пар. Не обладают свойством стационарности (не ходят вокруг одной оси(линии)).
Как определить коинтегрированную пару и тот самый коэффициент?
Для этого используется тест Engle-Granger.
Его алгоритм:
Шаг 1. Определить является ли цена(временной ряд цен) акции «А» за определенный период времени стационарной. Если НЕ является, то: Определить является ли сами по себе цены акции «В» стационарными. Если НЕ является, то переходим к шагу 2.
Шаг 2. Строим линейную регрессию пары А и B, и выделяем остатки (регрессии в отдельный ряд.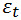 
Шаг 3. Проверяем на стационарность ряд «остатков» регрессии, если он стационарен, то два ряда цен коинтегрированы.
Теперь по порядку.
«Является ли цена акции «А» за определенный период времени стационарной».
Для определения является ли ряд стационарным (то есть сохраняются ли его вероятностные свойства на протяжении времени, или простыми словами ходит он вокруг некоторой линии или нет) используется тест ADF (Augmented Dickey Fuller test). Он наиболее популярен. О том как с ним можно познакомится укажу в конце статьи.
Для продвинутых: отсутствие стационарности это наличие единичного корня I(1), то есть интеграция первого порядка. Присутствие стационарности это отсутствие единичного корня I(0). Проверить можно любым unit root тестом.
«Строим линейную регрессию пары А и B, и выделяем остатки регрессии в отдельный ряд».
Регрессия – по простому это поиск зависимости между двумя временными рядами. То есть насколько нужно увеличить величину В, чтобы величина А увеличилась на единицу.
Помните изначальное выражение?
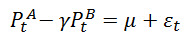
Если мы перенесем в правую сторону: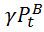
То получим:
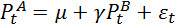
Это будет уравнение регрессии. Разберем подробнее.
Что такое регрессия?
Пример для понимания:
У нас есть два ряда данных:
- Ежедневная выручка продуктового магазина в течении месяца.
- Количество людей заходящих в магазин каждый день в течении месяца.
Очевидно что каждый человек тратит в магазине определенную сумму денег. Кто то больше, кто-то меньше. Однако практически всегда увеличение количества покупателей ведет к увеличению выручки. Для того чтобы определить как в среднем меняется выручка от количества зашедших людей и строится регрессионное уравнение. Где главное это итоговый коэффициент γ который и покажет насколько рублей в среднем изменится выручка если в магазин зайдет 1 дополнительный человек.
Но поскольку мы находим только «среднее\усредненное» значение, а каждый человек тратит разное количество денег в магазине, то мы будем постоянно иметь некоторое отклонение от прогнозируемого значения. Это значит что даже если в магазин будет заходить ровно 100 человек в день, выручка будет каждый день разной, хоть и колеблющейся вокруг одного значения. То есть со 100 человек мы можем прогнозировать выручку 100 тысяч рублей. Но в какой то день она будет 93 тысячи в другой 108 тысяч. Выручка разная, но колеблется вокруг 100 тысяч.
Так вот эта самая «ошибка» (разность) прогноза и реально полученной выручки, и называется остатком регрессии и обозначается как:
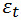
И чем лучше у нас построена линейная регрессионная модель (найден соответствующий коэффициент γ). Тем меньше будет «гулять» значение остатка. То есть тем меньше мы будем ошибаться в своих прогнозах.
Линейная регрессия строится с помощью Метода Наименьших Квадратов (МНК, на англ: OLS). Его суть в том, что он ищет то самое значение коэффициента γ так, чтобы ошибка (остаток) была минимальной.
Идем далее.
Итак у нас есть две акции А и B и их цены за период 2 года. Мы построили линейную регрессию и увидели что в среднем зависимость между ценами акций можно описать как:
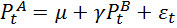
Где μ – это значение цены акции А, если значение цены акции В будет равно 0. Это просто константа (число которое не меняется во времени например оно может быть равно «3» или «298» или быть отрицательным).
Для того чтобы проверить являются акции коинтегрированными или нет, нам необходимо взять отдельно ряд остатков за некоторый период времени, например 2 года. Несмотря на то что мы вычислили как акции "в среднем" зависят друг от друга, напротяжении 2х лет цена, практически ежедневно, отклонялась от среднего. Мы берем эти отклонения отдельно, и также проверяем их на тест ADF (проверяем остатки на стационарность). И если этот ряд стационарен то цены А и В коинтегрированы.
Теперь к делу.
Что всё это значит и как торговать?
Мы можем предположить что если акции в течении 2х лет, коинтегированы (между их значениями есть некоторое равновесие), то скорее всего это равновесие будет сохранятся дальше. А мы можем торговать краткосрочные отклонения, от этого равновесия. Зная что в итоге они придут к своему долгосрочному равновесию. Что значит отклонение от равновесия? Это те самые остатки:
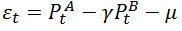
Поскольку эти отклонения стационарны, то мы можем надеется на то, что отклонившись от равновесия, остаток вернется к равновесному значению.
Еще раз поясню на картинке. В идеале график остатков должен выглядеть так:
Как мы можем видеть отклонившись от 0, через некоторое время он стабильно к нему возвращается. То есть значение легко прогнозируемо.
Стандартная реализация торговли это построение торговли на отклонении z-score.
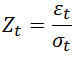
Дабы не сильно перегружать статью, скажу лишь что в статистике есть способ оценить разброс случайной величины от его среднего значения именуемый дисперсией. Корень из дисперсии называется Стандартным отклонением и обычно записывается как σ. Так вот z-score по сути измеряет текущее значение до равновесия в стандартных отклонениях.
Типичный график z-score выглядит так:
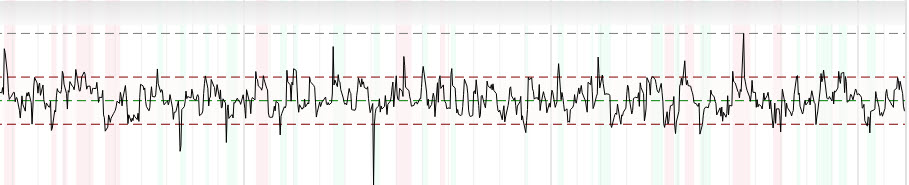
Соответственно отсюда строим стратегию:
- если Z-score≥2 (Красная пунктирная линия сверху) открытие короткой позиции по А, длинной по В где B берется в количестве равному коэффициенту γ, закрытие позиции при Z-score=0 (зеленый пунктир посередине);
- если Z-score≤-2 (Нижняя красная пунктирная линия) открытие длинной позиции по А, короткой по Вгде B берется в количестве равному коэффициенту γ, закрытие позиции при Z-score=0 (зеленый пунктир посередине);
По базе всё. Граница z-score от которой происходит вход, для некоторых пар может быть больше, может быть меньше, для её определения надо смотреть на исторические данные.
Теперь кратко о том как можно уже сейчас руками потрогать методики рассчета (вам придется погуглить):
- Для построения ADF и Engle-Granger можно воспользоваться пакетом EViews (на нем много чего интересного из эконометрики можно делать).
- Однако более удобно воспользоваться пакетом MATLAB или Rstudio (он может скачивать котировки прям с яху, и есть встроенная функция adf). Также они удобны тем что можно например сразу рассчитать скорость возврата спреда к равновесию. И соответственно заранее отбирать акции с более быстрой сходимостью. Что означает большее и более уверенное количество сделок.
- Построить регрессию также можно в EXCEL для этого надо подключить пакет анализа данных.
- Стандартное отклонение это функция =СТАНДОТКЛОН. Также она есть в thinkorswim.
Описанный выше коинтеграционный подход наверное самый простой. Но это только подход, данный для понимания, хоть и рабочий. Усложнять его Вам самим. Например регрессию и стд.отклонение нужно пересчитывать каждый день, то есть окно рассчета должно двигаться, для разных пар размер окна может быть разным. МНК можно заменить Total или любым другим методом. Можно предварительно работать с рядами цен для получения более точных входов. И фильтровать сам спред. И многое многое другое.
Также есть более интересные динамические модели расчета входов, для интрадея. И вероятностные подходы к стат арбитражу, которые сейчас в процессе теста.
P.S. Не забывайте комментить, поправлять и задавать вопросы.