В прошлой статье о коинтеграционном подходе, я кратко упоминул о том, что такое регрессия, и зачем она необходима в парном трейдинге. Для того чтобы чуть более наглядно показать суть регрессии, возьмем пример из предыдущей статьи. Итак у нас есть данные о количестве посетителей магазина каждый день, и ежедневная выручка в формате:
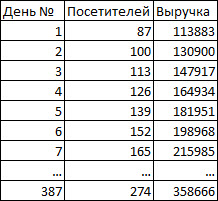
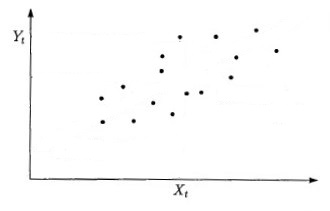
Нам необходимо определить как в среднем меняется выручка магазина в зависимости от количества посетителей. Нанесем каждый день данных, как точки на график, где за Х возьмем количество посетителей, а за Y количество покупателей.
Проведем линию которая предположительно описывает наши данные.
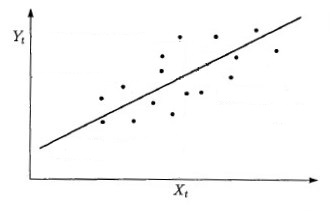
Чтобы понять насколько точно проведенная линия описывает зависимость наших данных. У нас есть два варианта: Подсчитать сумму модулей отклонений точек до линии. Или подсчитать сумму квадратов этих отклонений.
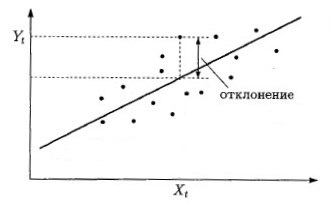
Мы выберем второй вариант, поскольку подсчет модулей дает неоднозначные результаты (сумма модулей может быть одна и та же, а кривые разные).
Подсчитаем сумму квадратов отклонений от наших наблюдений до проведенной линии.
Затем проведем еще одну линию, и если сумма отклонений от этой линии будет меньше. То мы выберем её. Так пока не найдем линию, где сумма квадратов отклонений будет наименьшей. Угол наклона будет коэффициентом гамма β (иногда называют гаммой γ) в регрессионном уравнении:
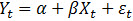
Примерно так выглядит суть (подчеркиваю) метода построения регрессии.
Наиболее распространенным и простым методом построения регрессии является Метод Наименьщих Квадратов (МНК. От англ OLS). Однако часто использование МНК может привести к ошибкам связанным с тем, что метод расчёта МНК является несимметричным. Что это значит?
Это значит что регрессия где количество посетителей будет независимой переменной, зачастую будет отличаться от регрессии построенной по тем же данным, но с количеством выручки в качестве независимой переменной.
Иначе говоря:
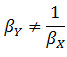
Это происходит оттого что в МНК учитывается только вариативность одной переменной и единственный источник дисперсии, а вторую считает константой с нулевой дисперсией.
Например:
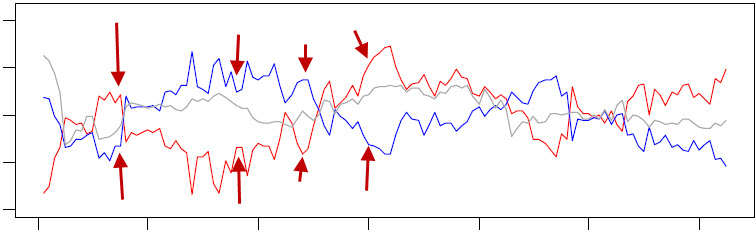
По логике вещей спреды должны быть зеркальными, но этого не происходит. Стрелочками выделил где отчетливо видно несоответствие. Это значит что лонг по Х, шорт по Y, не тоже самое что шорт по Х и лонг по Y.
Исправить ситуацию может использование ортогональной регрессии (TLS, EIW, Deming regression), неё бета получается зеркальной. Хотя сами алгоритмы рассчета немного сложнее.
Вот такая короткая статья, мысли в слух. Готовлю к работе (вспоминаю) методику стохастика.
А сегодня в 19:00, всем кто интересуется парным трейдингом, необходимо быть здесь:
http://utmagazine.ru/posts/6795-vebinar-po-parnomu-treydingu-18-marta-v-sredu (!!!)