Модель Блэка-Литтермана максимально простым языком (часть 1)

Поговорим еще немного про портфели. Я окончательно решил изменить формат статей из рубрики ресечинговых на более неформальный, поэтому здесь будет встречаться речь от первого лица (то беж от меня), фразы будут более неформальными, а также я буду приводить собственные рассуждения и примеры из личного опыта. Сразу хочу попросить прощения у читателей за задержку материала с примером портфеля по индексной модели Шарпа, я готовлю этот материал, однако перед этим выложу еще одну, на мой взгляд, очень важную статью из серии портфельного менеджмента. На сей раз речь идет о модели Блэка-Литтермана – принципа построения портфелей на основе оптимизационной модели Марковица с применением более глубокой диверсификации. Сразу скажу, тема эта очень сложная и для меня во многом экспериментальная, на практике я этот принцип построения портфелей никогда не применял, хотя многие ее элементы так или иначе использовал. Поэтому я решил разбить материал этой темы на две части. Если у кого-то будут вопросы по первой части материала, можете писать их в комментариях под статьей или в рубрике «задай вопрос аналитику».

Начнем с небольшой теоретической вводной. Данная модель построения портфелей была предложена выдающимися экономистами в сфере финансовых рынков – Фишером Блэком и Робертом Литтерманом, и представляет собой метод построения эффективного инвестиционного портфеля на основе оптимизационной модели Гарри Марковица, который в то же время решает многие недостатки последней благодаря применению более глубокой диверсификации. В целом данная модель представляет из себя комбинацию модели CAPM и задачи обратной оптимизации Шарпа, а также оптимизационной модели Марковица. Отличительной особенностью данного портфеля является оптимальный анализ рисков и потенциальной доходности отбираемых активов при распределении долей. Однако отбор всех параметров, необходимых для данной модели, довольно сложный и трудоемкий процесс и без соответствующей материально-технической базы сделать это не представляется возможным. Поэтому ряд вводных параметров я вынужден буду опустить, несмотря на то, что это негативно повлияет на качество модели.

Ключевым элементом модели Блэка-Литтермана является учет потенциальной доходности активов. И поскольку первоначально предложенный принцип вектора доходности был крайне чувствителен к текущей конъюнктуре рынка и даже при минимальном отклонении изменял структуру портфеля на 50%, создатели данной модели предложили использовать регрессионный анализ на основе исторических данных котировок. Для более глубокой диверсификации, создатели модели взяли принципы построения по Тобину, который предполагает использование в том числе и коротких позиций для достижения приемлемых уровней риска и сохранения желаемой потенциальной доходности.

В модели Блэка-Литтермана в качестве стартовой нейтральной позиции были выбраны «равновесные» доходности активов (то есть доходность с учетом их доли в портфеле). Вектор равновесной доходности активов можно рассчитать формулой обратной оптимизации по Шарпу:

V=lSwmkt, где

V – вектор равновесной доходности активов,

l - коэффициент склонности инвестора к риску,

S - ковариационная матрица доходностей активов,

wmkt – удельный вес каждого актива в портфеле.

Теперь необходимо сформировать оптимизационную модель портфеля по Марковицу. Для начала стоит сразу выделить ограничения: запрет на короткие сделки и использование плеча. Кроме того, существует также ограничение по рискам, в частности показателя VaR и ограничение доли одного актива в портфеле. Таким образом, формируется портфель по стратегии “Only long”. Основной целью в данном случае является курс на максимизацию доходности вложений с учетом выше названных ограничений. В итоге, формула оптимизационной модели портфеля принимает вид:

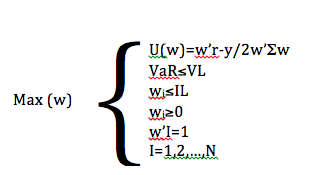Где N – количество активов в портфеле;

w – вектор-столбец, определяющий аллокацию портфеля;

r – вектор-столбец, содержащий ожидаемые доходности инструментов;

S – ковариационная матрица доходностей инструментов;

g – коэффициент толерантности к риску;

VaR и VL – максимальный уровень потерь портфеля и соответствующий лимит;

IL – индивидуальный лимит для вложения в один инструмент,;

I – единичная матрица.

Переходы к практической части реализации оптимизационной модели, сначала необходимо сформировать исходные данные. Первоочередной задачей является определение метрик, характеризующих доходность финансовых активов и их волатильность. Поскольку стандартные показатели математического ожидания, дисперсии и стандартного отклонения являются неприемлемыми для модели Блэка-Литтермана, их необходимо заменить на экспоненциально-взвешенное среднее математическое ожидание, волатильность и ковариационную матрицу. Если предположить, что на определенный момент времени t портфель состоит из N-количества акций, а цены этих акций условно обозначить как p₁, p₂,…,p_n, а также учесть, что котировки по каждому активу формируют временные ряды глубины T (pjt,…,p_jt-i,…,p_jt-T), то формула расчета доходности акции за период i на момент времени t следующая:

r_jt=ln p_jt/p_jt-1 – rf_t(i), таким образом r_jt~N(r’_jt,s²_jt), где

r’_jt - оценка математического ожидания доходности в момент времени t;

s²jt – оценка дисперсии доходности актива в момент времени t;

rf (i ) t – уровень безрисковой ставки на момент времени t, получаемая на основе доходности ОФЗ и публикуемой Московской биржей кривой безрисковой ставки доходности к сроку i.

Тут стоит немного выдохнуть, так как первая часть этого материала закончена. Во второй части я постараюсь до конца разобрать оптимизационную часть модели, в общих чертах описать определение доходности активов с учетом рыночных данных и экспертных оценок. В последующем постараюсь собрать экспериментальный портфель по модели Блэка-Литтермана.