Итак, продолжаем изучение модели Блэка-Литтермана. Как я и обещал, материал этот будет разбит на 2 части и эта статья заключительная по этой теме. В конце данного материала будет разложен пример с использованием данной модели – сразу скажу, пример этот я лично не использовал (повторюсь изучение этой модели для меня тоже является неким экспериментом), а нашел как вторичную информацию в интернете. Продолжим без предисловий.
Использование логарифмической доходности интуитивно понятно и это дает нормальное распределение стоимости акции. Безрисковая ставка играет роль стабилизатора и фильтра неэффективных вложений, поскольку если тот или иной актив с определенным уровнем риска обладает доходностью ниже безрисковой, то в этом случае актив считается неэффективным. Иными словами, если тот или иной рисковый актив не предусматривает премии за риск, то в этом случае инвестиции в него не являются актуальными.
Крайне важным в данной модели является использование не простого метода исчисления ключевых параметров портфеля (то беж ковариации, вариации, математического ожидания и т.д.), а экспоненцильного – то есть расчета тех или иных показателей исходя из ретроспективы. Таким образом, формулы расчетов ключевых показателей инвестиционного портфеля – ожидаемой доходности, волатильности и ковариации – на определенный момент времени t соответственно выглядят следующим образом:
r’jt=(1-l)åTi=1li-1rjt-i+1;
s=((1-l)åTi=1li-1(rjt-i+1-åirji/T))1/2;
covmnt=(1-l)åTi=1li-1(rmt-i+1-åirmi/T) (rnt-i+1-åirni/T)
Далее для определения параметра l применяют т.н. уровень лояльности j, формула для расчета которого следующая:
jt=lT(1-l)(1+l+l2…+ln), или jt=(1-l)å¥t=Tlt
Таким образом, индекс лояльности представляет из себя сумму весов данных, находящихся вне горизонта T, и из этого вытекает формула расчета последнего:
T=lnjt/lnl.
После определения основных метрик доходности и волатильности, а также степени риска активов, необходимо рассчитать индекс лояльности инвесторов к риску того или иного актива. Данный показатель используется как в оптимизационной модели, так и в модели Блэка-Литтермана, и применяется для дальнейшего расчета равновесного вектора доходности инструмента. Индекс указывает на то, какую премию инвестор готов получить дополнительно за увеличение риска g портфеля на какую-либо величину. Для нахождения показателя необходимо сделать регрессивный анализ доходности бенчмарка – в данном случае, поскольку мы уже начали говорить про российский рынок в сегменте национальной валюты, таковым является индекс ММВБ. Поскольку портфель формируется в определенный момент времени, то как отмечалось выше, для эффективного расчета ожидаемых показателей доходности и риска должен использоваться экспоненциально-взвешенный метод:
gt=rat/s2t(ra), где
ra – избыточные логарифмические доходности бенчмарка.
Все это выглядит, конечно, довольно сложно, но если разобраться на практике, то по сути вполне преодолимо даже для не владеющего финансовой математикой на профессиональном уровне. Во время разбора конкретного примера по данной модели, думаю, многое станет понятно. Продолжим…
После определения индекса лояльности инвесторов к риску стало, наконец, возможно рассчитать вектор комплексной доходности по модели Блэка-Литтермана. Первый этап – определение вектора равновесной доходности. Формула расчета следующая:
raПt=gtåtwcapt, где
gtåt – ковариационная матрица на момент времени t;
wcapt – N-мерный вектор-столбец долей активов, входящих в портфель.
И далее уже после расчета вектора равновесной избыточной доходности стало возможным вычислить ключевой показатель для реализации модели – комплексный вектор ожидаемой доходности. Выражение комплексный означает использование вектора доходности несколькими методами, которые взаимодополняют друг друга. В данном случае для формирования комплексного вектора, мы будем использовать вектор ожидаемой и равновесной доходности. Таким образом, равновесную доходность мы скорректируем по ожидаемым показателям доходности с учетом экспоненциальной составляющей. Согласно модели Блэка-Литтермана, комплексный вектор доходности рассчитывается исходя из следующей формулы:
r(П, r’)=[å-1+P’WP]-1[å-1П+P’Wr’], где
П – вектор равновесной доходности;
r’ – экспоненциально-взвешенный средний вектор ожидаемой доходности;
å - матрица экспоненциально-взвешенных ковариаций;
P – квадратная NxN матрица согласования вектора прогноза и конкретного актива;
W - матрица уверенности инвесторов в конкретном прогнозе актива.
Из всего перечисленного не хватает только матрицы уверенности инвесторов в прогнозе W. Чтобы вычислить и этот показатель, необходимо построить матрицу, основанную на ковариационной матрице. Это будет наиболее простым и интуитивно понятным в рамках модели Блэка-Литтермана – ковариации активов будут объяснять отклонение доходности от среднего значения (то есть показатель стандартного отклонения), а значит объяснять ошибку прогноза. А поскольку прогнозы формируются на основе абсолютных указаний и корреляция между ними должна полностью отсутствовать (то есть быть равной 0), то на момент времени t могут быть сформированы соответственно матрицы P и W. В первом случае матрица P принимает вид единичной диагональной матрицы I, а матрица W также является квадратной размерности NxN и диагональной, но на диагонали которой находятся экспоненциально-взвешенные дисперсии:
W=[s2j]
Таким образом, распространение ошибки прогноза является нормальным с нулем в качестве математического ожидания и матрицей W в качестве ковариационной. В результате, вектор ожидаемой доходности на основе средних значений будет добавлять к вектору равновесной доходности дополнительные премии с учетом экспоненциально-взвешенной составляющей их расчета с коррекцией на волатильность. При этом прогноз по каждому инструменту будет осуществляться по отдельности вне зависимости от влияния на структуру портфеля. С учетом нашего подхода при рассмотрении данной модели, для комплексного вектора доходности первого уровня можно сохранить принцип нормального распределения с текущими параметрами t:
r»N(r, å).
В данной модели существует еще один элемент – преобразование комплексного вектора доходности при помощи экспертных оценок. Однако ввиду того, что источники таких оценок, да и сами оценки подвержены многочисленным нерыночным ошибкам, я решил этот шаг пропустить. Собственно и все, теоретическая часть модели Блэка-Литтермана рассмотрена. В качестве дополнительной меры по минимизации рисков можно также ввести ограничение на величину ожидаемых потерь – показатель VaR, однако в данном материале мы подробно на этом останавливаться не будем, так как этот показатель будет подробно рассмотрен в отдельной статье. Мы же перейдем сразу к практике модели Блэка-Литтермана, а именно – построению инвестиционного портфеля. Я еще раз повторюсь, что у меня нет практического опыта использования этой модели в портфельном менеджменте и ее рассмотрение в данном материале для меня экспериментально. Более того – пример построения портфеля также взят из научной статьи. Однако этого вполне достаточно, чтобы понять как самостоятельно при желании или необходимости построить инвестиционный портфель по этой модели, так как подготавливая данный материал у меня не было цели что-то кому-то доказать, а просто объяснить понятным даже для начинающих трейдеров и инвесторов языком о принципах его функционирования и построения.
Поскольку в данной статье мы уже коснулись российского рынка, то и портфель будет сформирован исходя из российских финансовых инструментов. Еще раз повторюсь – данный портфель я самостоятельно не формировал (для этого необходимо иметь хорошую техническую подготовку и материально-техническое обеспечение – ни того, ни другого у меня нет), а просто разобрал пример из сети. Для формирования портфеля были взяты реальные данные из 12 российских акций с ежедневной перелокацией активов в период с 11.01.2009 по 1.03.2012. Расчеты параметров для модели по отобранным активам в данном примере происходил с использованием написанных программных кодов на языке VBA в известной программе Excel. Для оптимизации использовалась настройка программы - Excel-Solver Table.
В рамках данного примера установлены следующие параметры:
глубина расчета доходности в размере I=10;
показатель l в соответствии с рекомендациями Risk Metrics – 0.94;
глубина рестроспективы при допустимом уровне ошибки в 0.00001% в горизонте 1 год составляет T=250 наблюдений;
количество степеней свободы для уровня максимальных потерь n=33;
вероятность уровня максимальных потерь a=5%;
лимит максимально допустимых потерь для инвестора VL=15%;
аналогичный лимит и для предельно допустимых потерь по каждому отдельному инструменту IL=15%.
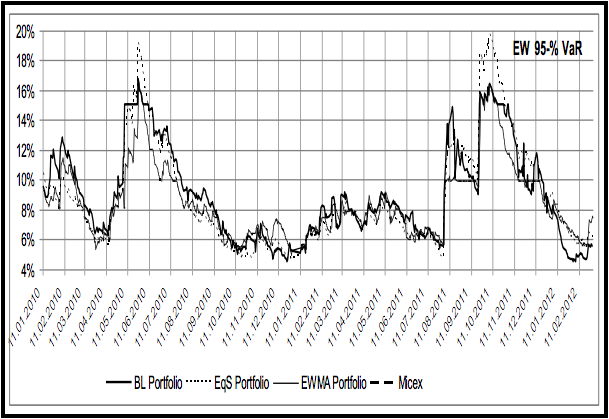
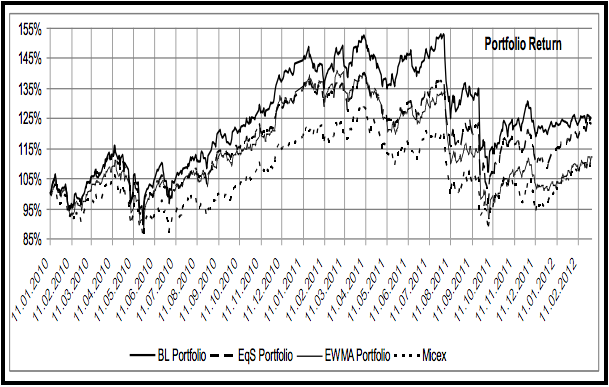
Далее по формуле Rt=Rr-1(1+W*t-1’rt), где W*t-1 – аллокация активов, рассчитывается цепной индекс доходности. Тем самым оценивается эффективность работы аллокации активов, построенная на основании текущего прогноза. Далее внизу представлены графики цепных доходностей рассматриваемых портфелей и оценки их максимальных потерь.
Как видно из графиков, доходность рассчитанного в рамках данной модели портфеля превосходит аналоги и динамику бенчмарка. При этом стоит отметить ряд особенностей – данная модель наиболее эффективно работает на бычьем рынке, а оценка уровня максимальных потерь даже в случае пробития лимита быстро корректируется в рамках перелокации в более безопасные активы. При этом, по итогам более чем 2-летнего тестирования, портфель по модели Блэка-Шоулза показал значительно более высокую доходность по сравнению с индексом ММВБ и при сопоставимых рисках доходность данного портфеля выше по сравнению с аналогами.
На этом собственно и все. Материал был сложный, но я надеюсь что сумел передать его изложение максимально простым языком. Если еще остались какие-то вопросы, их можно задать в комментариях под статьей либо в рубрике “задай вопрос аналитику”.


Где это рубрика такая про задай вопрос?