Как уже говорилось в предыдущей статье основ формирования инвестиционных портфелей, существуют различные модели формирования портфелей http://utmagazine.ru/posts/5285-post-547aefcf30174
Как и было обещано, на сей раз мы разберем модель формирования портфеля ценных бумаг по модели еще одного выдающегося американского экономиста – Джеймса Тобина. Сразу отметим, что конкретно в этой статье будут рассмотрены теоретические основы и основные принципы портфельной теории Тобина и в конце будут даны несколько практических советов. В следующей статье из этой же серии будут рассмотрены непосредственно действия для самостоятельного построения портфеля ценных бумаг по модели Джеймса Тобина.
Итак, есть два ключевых отличия модели Тобина от модели Марковица: использование т.н. «безрисковых активов», дающих определенную доходность без риска просадки (чаще всего это облигации или банковские депозиты); и возможность применения коротких сделок наряду с длинными (в модели Марковица применяется стратегия «only long»). Таким образом, в модели Джеймса Тобина при отборе инвестиционных инструментов не требуется применять фильтрацию по факторы потенциальной просадки.
Кроме того, важным отличием является также и то, что в отличие от модели Марковица или скажем Блека, в данной модели больший акцент делается на структуре рынка, нежели структуре допустимых портфелей. Т.е. иными словами – классификация возможных активов более широкая и может включать даже синтетические опционные позиции. Однако есть одно ограничение – сумма всех долей позиции должна быть равна 100%, включая долю безрисковых активов и синтетических сделок. Это позволяет хеджировать целый ряд рисков и даже сформировать т.н. «Бета-нейтральный портфель» (об этом будет рассказано в следующих статьях).
Доходность портфеля по Тобину будет равняться общей доходности всех инвестиционных инструментов, включенных в него, в том числе безрисковых. Собственно достижение этой доходности представлено следующей формулой.
Таким образом, ключевым фактором при формировании портфеля по Тобину является отбор наиболее потенциально доходность инвестиционных инструментов. В качестве расчета для риска инструмента используется показатель стандартного квадратического отклонения каждого торгового инструмента. Кроме того, для снижения рисков доходности портфеля необходимо также сформировать корелляционную матрицу из выборки торговых инструментов, чтобы отобрать наименее кореллируемые активы.
Далее постараемся разобраться в экономико-математической модели формирования портфеля с минимальным риском. Она представлена следующей формулой
Стоит отметить, что все вычисления по рискам делаются только для рисковых активов. В случае с безрисковыми активами рассчитывать показатели доходности или стандартного отклонения бессмысленно, поскольку цена на них не меняется за какой-либо временной промежуток. Поэтому формула меняется:
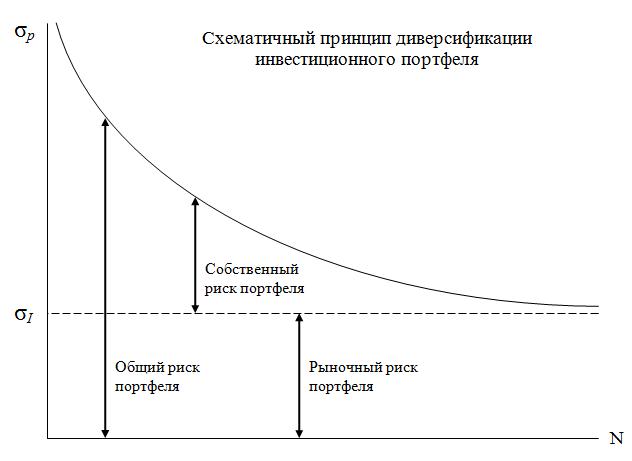
Стоит также отметить, что модели Тобина структура рисковой части портфеля зависит от требуемой потенциальной доходности актива. Исходя из этого в дальнейшем рассчитывается соотношение доли рисковых инструментов и безрискового актива. В результате, средняя доходность рисковой части портфеля высчитывается по формуле:
И наконец, стандартное отклонение эффективного портфеля, с учетом доли безрискового актива, рассчитывается исходя из следующей формулы:
Определить связь между средней ожидаемой доходностью портфеля и отдельных его активов, думаю, будет несложно. И наконец мы получаем, что если инвесторы рациональны, то рыночный портфель условно считается эффективным, а соответственно средняя доходность данного портфеля связана с доходностью рынка в целом линейной формулой:
Данная модель оценки активов более известная как CAPM. Пугаться тут ничего не стоит, несмотря на обилие сложных формул, сформировать портфель Тобина будет не так уж сложно. Для этого достаточно в Excel выполнить алгоритм действий, о которых будет рассказано в следующей статье. Ниже приведен пример оценки актива с помощью модели CAPM.
В таблице более наглядно продемонстрировано как можно самостоятельно рассчитать оценку того или иного актива с помощью модели CAPM.
Опять же пугаться тут ничего не нужно, на самом деле при выполнении определенного алгоритма действий все эти формулы знать будет и необязательно. Цель данной статьи была подготовить теоретическую базу для дальнейшей практики. В дальнейшем, кроме модели Тобина, будут также рассмотрены портфельные модели Блека-Литтермана, индексная модель оценки риска Шарпа, более подробно рассмотрена модель оценки активов CAPM, а также рассмотрена теория и практика модели дисконтированных денежных потоков.




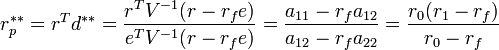



Будут примеры реальной работы этого?