Продолжаем цикл статей про портфели ценных бумаг. На сей раз рассмотрим то, как необходимо наиболее подробно и грамотно рассчитать эффективность работы портфеля. Ведь кроме умения правильно составлять, надо еще постоянно отслеживать действующий портфель и правильно рассчитывать его эффективность. Сразу условимся, что рыночной доходностью является доходность индекса S&P500.

На первый взгляд может показаться, что ничего сложного тут нет. Достаточно лишь рассчитать доходность портфеля и каждого актива и отсеить те активы, которые показали отрицательную доходность. Однако кроме доходности и простейших индикаторов вроде дисперсии, необходимо также рассчитать множество индикаторов рискованности портфеля и каждого актива в отдельности, чтобы понять с чем дальше работать и стоит ли вообще продолжать портфель. На самом деле существуют десятки показателей, которые так или иначе показывают эффективность и доходность портфеля, а также уровни риска.
Итак, условно показатели эффективности портфеля можно разделить на две группы: индикаторы доходности и индикаторы риска. К показателям доходности относятся следующие индикаторы: доходность каждого актива; доходность портфеля в целом; доходность безрискового актива; отношение доходности портфеля к рынку; отношение доходности портфеля к доходности безрискового актива.
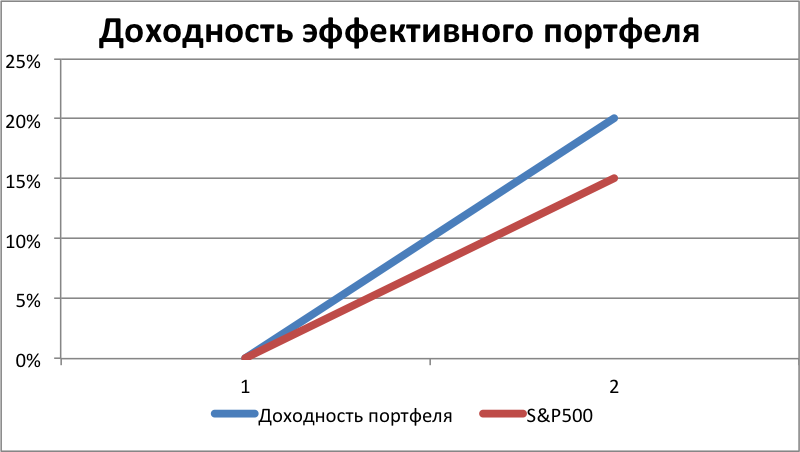
Считается, что портфель считается эффективным, если доходность превышает среднюю по рынку. Например, если доходность портфеля ценных бумаг «А», состоящий преимущественно из акций индекса S&P500, составила 20% годовых, а доходность самого индекса лишь 15%, то такой портфель считается эффективным.
Среди показателей риска выделяются следующие: стандартное отклонение доходности портфеля и каждого актива в отдельности от доходности рынка; коэффициент Шарпа; коэффициент бета; коэффициент Трейнора; Альфа Дженсена; коэффициент Швагера; коэффициент Сортино; М-квадрат. Как видно, показателей рисков гораздо больше, нежели доходностей, поскольку для инвесторов (в особенности крупных) более важным является сохранение средств, а уж затем приумножение.

Тут наверное многие занервничали и подумали, что все это очень сложно для них и, вероятно, надо заняться чем-нибудь другим. Но без паники! Для начала разберемся в определениях перечисленных показателей. Если с показателями доходности еще все понятно, то по рискам было бы неплохой кратко дать разъяснение.

Стандартное отклонение – средняя разница моментной доходности портфеля от доходности рынка за определенный период, обычно обозначается значком . Например, при дневной доходности портфеля в 2% и дневной доходности рынка 1.5% за месяц торговли, стандартное отклонение доходности составляет 2%-1.5%=0.5%. Чем выше стандартное отклонение, тем более рискованным считается портфель.

Коэффициент Шарпа – отношение средней премии за риск к стандартному отклонению портфеля. Иными словами, это разница в доходности портфеля к безрисковому активу, деленная на стандартное отклонение портфеля. Формула довольно простая: при доходности портфеля 2%, стандартному отклонению 0.5% и доходности безрискового актива в 0.4%, коэффициент Шарпа равен (2%-0.4%)/0.5%=3.2. Считается, что чем больше данный коэффициент, тем более успешным было управление портфелем.

Коэффициент бета – скорость изменения доходности портфеля по сравнению с доходностью рынка, обычно обозначается . Т.е. иными словами, данный коэффициент показывает как сильно изменяется доходность по сравнению с доходностью рынка в целом. Для расчета этого индикатора достаточно лишь два показателя: ковариация портфеля и рынка (произведение сумм корелляции и стандартного отклонения портфеля и рынка) и дисперсия доходности рынка (рассчитывается как стандартное отклонение в квадрате).
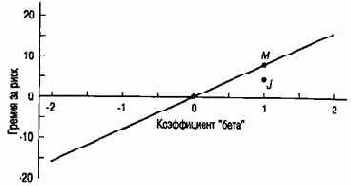
Например, при корелляции портфеля с рынком 0.7, стандартного отклонения рынка 0.3% и стандартного отклонения портфеля 0.5%, получается ковариация 0.7*0.3%*0.5%=0.0000105. Дисперсию же рассчитать довольно просто: 0.3%^2=0.000009. Отсюда находим бета-коэффициент 0.0000105/0.000009=1.16667. Коэффициент бета больше 1 как правило указывает на более рискованный характер портфеля.
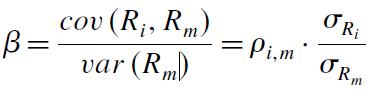
Теперь рассчитаем коэффициент Трейнора – это показатель отношения премии за риск и самого риска портфеля. Иными словами это отношение разности доходности портфеля к рынку и деленная на коэффициент бета. Формула довольно простая – при полученных выше показателях получается следующий расчет: (20%-15%)/1.16667=0.04285. Чем выше коэффициент Трейнора, тем более эффективным считается портфель. Значение этого коэффициента ниже 0% свидетельствует о том, что портфель либо менее доходный чем рынок, либо что имеет вовсе отрицательную доходность.

Альфа Дженсена – коэффициент, предложенный американским экономистом Майклом Дженсеном в 1968 году и показывающий, насколько эффективно активное управление портфелем по сравнению с пассивным. Для его расчета необходимы 4 показателя: средняя доходность портфеля (2%), средняя доходность рынка (1.5%), доходность безрискового актива (0.4%) и коэффициент бета портфеля (1.16667). Формула для расчета следующая: 2%-(0.4%+(1.5%-0.4%)*1.16667)=0.32%. В данном случается получается, что среднедневная доходность портфеля на 0.32% выше, чем в среднем по рынку. Чем больше значение данного коэффициента, тем более эффективно управляется портфель. Значение коэффициента ниже 0 указывает на то, что доходность рынка выше, чем доходность портфеля.
![]()
Коэффициент Швагера – отношение прибыли портфеля к средней максимальной просадке за определенный период (как правило берут годовые данные). Был предложен известным экономистом Джеком Швагером. Формула довольно простая: при среднегодовой доходности портфеля в 100 тыс. долларов и максимальной просадке 25 тыс. долларов, получается 100/25=4. Это означает, что среднегодовая прибыль портфеля в среднем в 4 раза большая, чем максимальная просадка.

Коэффициент Сортино очень похож на коэффициент Шарпа и указывает на эффективность управления портфелем. Разница лишь в том, что данный показатель вбирает в себя только те значения доходности, которые ниже определенного уровня. Как правило, в качестве такого уровня берется доходность безрискового актива. Формула расчета использует всего три показателя: среднедневная доходность инвестиционного портфеля (2%), минимально допустимая дневная доходность (дневная доходность безрискового актива – 0.4%/280=0,0014%) и количество дней ниже минимально допустимой доходности (условно возьмем этот показатель 15). Рассчитывается следующим образом: (2%-0.0014%)/15=0.0013. Данный коэффициент характеризует эффективность управления портфелем в периоды спада рынка.

Наконец, последний коэффициент М-квадрат или просто М2 указывает на то, насколько более высокую доходность показывает портфель, по сравнению с безрисковым активом. Данный коэффициент был предложен в 1997 итальянским экономистом Модильяни. Для его расчета требуются четыре показателя: средняя доходность портфеля (2%), средняя доходность безрискового актива (0.0014%), стандартное отклонение доходностей портфеля (условно возьмем 1%) и стандартное отклонение доходности рынка (условно возьмем 0.5%). Формула следующая: (2%-0.0014%)*0.5%/1%+0.0014%=10%.

Собственно и все. Рассчитать приведенные выше показатели эффективности инвестиционного портфеля оказалось не так сложно, как могло показаться на первый взгляд, хотя это и занимает достаточно много времени. Но наверное все согласны с тем, что это время стоит того, чтобы наиболее точно рассчитать эффективность вложений в тот или иной портфель и максимально минимизировать возможные риски. В следующей статье будет приведет пример расчета данных показателей в Excel.