Как рассчитать эффективность портфеля ценных бумаг в Excel

Как и было обещано в предыдущей статье, в этой будет рассказано о том, как рассчитать основные показатели эффективности инвестиционного портфеля непосредственно в Excel http://utmagazine.ru/posts/5908-kak-rasschitat-effektivnost-portfelya-cennyh-bumag

Мы уже выяснили, что несмотря на казалось бы сложные термины и индикаторы, рассчитать эти индикаторы на самом деле не так уж и сложно. В случае с расчетами в Excel эти расчеты делать будет еще проще, так-как процесс в целом автоматизирован. Необходимо лишь грамотно расставить ячейки и сделать ссылки на соответствующие ячейки. И поскольку с показателями доходности в целом все понятно, рассматриваться будут лишь расчеты индикаторов риска.

Так как в предыдущей статье уже были определения основным индикаторам риска, в данном случае, чтобы не перегружаться лишней информацией, речь будет идти лишь о самих расчетах. Обо всем по порядку.

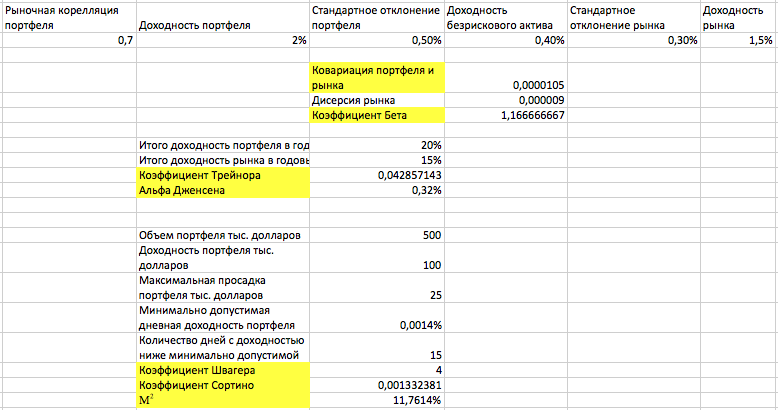
На всякий случай повторим основные показатели риска: стандартное отклонение доходности портфеля и каждого актива в отдельности от доходности рынка; коэффициент Шарпа; коэффициент бета; коэффициент Трейнора; Альфа Дженсена; коэффициент Швагера; коэффициент Сортино; М-квадрат. По очереди теперь разберемся с расчетом каждого из этих индикаторов в Excel. Стоит наверное всех обнадежить – сделать это довольно просто, по крайней мере гораздо легче, чем может показаться на первый взгляд. Более того, в случае расчетов в Excel достаточно просто использовать соотвтетсвующие функции. Сразу оговоримся, что все цифры условные и взяты из предыдущей статьи.

Стандартное отклонение – самый простой из всех показателей для расчетов. Для его расчета необходима лишь доходность портфеля относительно рынка. Необходимо лишь в соответствующую ячейку вставить формулу «СТАНДОТКЛОН.В(…)» и выбрать соответствующий массив данных по доходности.

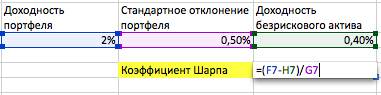
Коэффициент Шарпа – разница в доходности портфеля к безрисковому активу, деленная на стандартное отклонение портфеля. Формула рассчитывается просто: при доходности портфеля в 2% и полученному стандартному отклонению 0.5%, а также и доходности безрискового актива в 0.4%, необходимо от первой ячейки отнять вторую и все это разделить на третью.

Коэффициент бета – скорость изменения доходности портфеля по сравнению с доходностью рынка. Соответственно необходимо математически рассчитать насколько доходность рынка влияет на доходность портфеля. Формула используется лишь два показателя: ковариация портфеля и рынка (произведение сумм корелляции и стандартного отклонения портфеля и рынка) и дисперсия доходности рынка (рассчитывается как стандартное отклонение в квадрате).

Для начала рассчитаем коэффициент ковариации. При корелляции портфеля с рынком в 0.7, стандартного отклонения рынка 0.3% и стандартного отклонения портфеля 0.5%, получается ковариация 0.7*0.3%*0.5%=0.0000105. Для расчета дисперсии рынка достаточно стандартное отклонение возвести в квадрат: 0.3%^2=0.000009. Отсюда находим бета-коэффициент 0.0000105/0.000009=1.16667.

Из полученных данных теперь рассчитаем коэффициент Трейнора – отношение премии за риск рынка и самого риска портфеля. Для его расчета требуется всего три показателя: общая доходность рынка, общая доходность портфеля и бета-коэффициент портфеля. При полученных выше показателях получается: (20%-15%)/1.16667=0.04285.

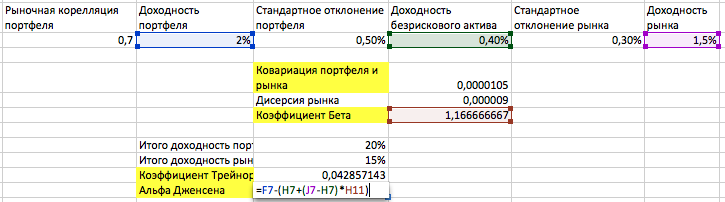
Альфа Дженсена – коэффициент, показывающий, насколько более эффективно активное управление портфелем по сравнению с пассивным. Для расчета необходимы 4 показателя: средняя доходность портфеля (2%), средняя доходность рынка (1.5%), доходность безрискового актива (0.4%) и коэффициент бета портфеля (1.16667). Чем больше значение данного коэффициента, тем более эффективно управляется портфель.

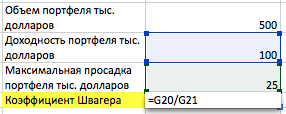
Коэффициент Швагера – отношение прибыли портфеля к средней максимальной просадке. Мы условно взяли данные за год при объеме портфеля в 500 тыс. долларов. Для расчета необходимо всего два показателя: среднегодовая доходность портфеля (500*0.2=100 тыс. долларов) и максимальная просадка (условно возьмем 5%: 500 *0.2=25 тыс. долларов). Далее делаем расчет по формуле.

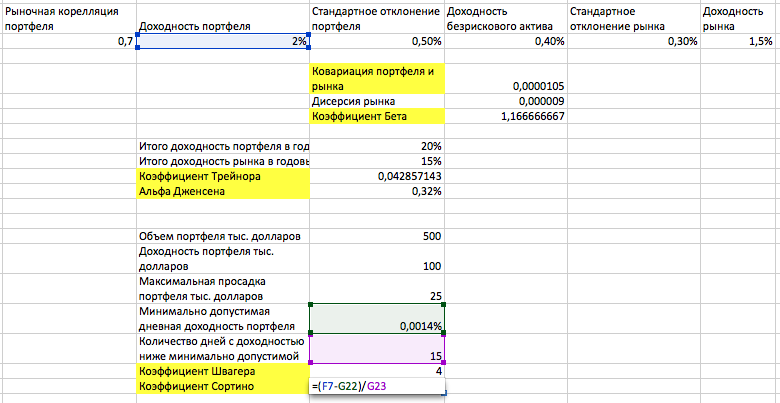
Коэффициент Сортино, также как и показатель Шарпа, указывает на эффективность управления портфелем, но не ниже минимально допустимой доходности. Для начала рассчитаем минимально допустимую доходность. Как правило, за такой показатель берется доходность безрискового актива (0.4%). Таким образом, с учетом количества рабочих дней в году (условно 280) минимально допустимая дневная доходность составляет 0.4%/280=0,0014%.

Далее необходимо количество дней ниже минимально допустимой доходности (условно возьмем этот показатель 15). После этого можно рассчитать непосредственно сам коэффициент Сортино. Рассчитывается следующим образом: (2%-0.0014%)/15=0.0013.

Наконец, последний коэффициент – М-квадрат или просто М². Данный индикатор указывает на то, насколько более высокую доходность показывает портфель, по сравнению с безрисковым активом. Для расчета требуются четыре показателя: средняя доходность портфеля (2%) и безрискового актива (0.0014%), стандартное отклонение доходностей портфеля (условно возьмем 1%) и стандартное отклонение доходности рынка (условно возьмем 0.5%).

Вот и все. Расчет всех эти коэффициентов в Excel оказался не таким уж и сложным, как и было обещано в начале статьи. После освоения этих двух материалов надеемся, что ключевые элементы портфельного анализа были успешно освоены.